‍

In 1712, Thomas Newcomen, a Baptist preacher and ironmonger from Dartmouth, Devon, constructed his newly designed “atmospheric engine” for Coneygree Coalworks. Each stroke of the 20-ton machine would raise about 37 liters of water from the flooded mines below. It worked continuously and without tiring, unlike the dozen horses it replaced.

Like those horses, however, Newcomen’s engine needed to be fed, burning copious amounts of the very coal that it was helping to unearth. Although these engines were cost-effective compared to horses or humans, they were still expensive to operate, and improvements to their efficiency were especially sought after.

In 1763, while working as a mathematical instrument maker at the University of Glasgow, James Watt was tasked with repairing the university’s scale model of the Newcomen engine. As he worked, Watt envisioned ways to improve the efficiency of the design. In 1776, he unveiled an engine with seemingly extraordinary modifications: it consumed 75-80 percent less fuel than Newcomen’s. Tasks that would have burned 100 kilograms of coal could now be done with a mere 20.

Although a triumph of engineering, Watt’s engine was nowhere near its optimal performance. The difference between Newcomen's and Watt’s engines, in fact, is between 0.5 percent and 2.5 percent efficiency. But these inventors could not have known this because the concept of a theoretical limit — asking how efficient an engine design could be, in principle — had not yet been imagined.

What was missing was a notion we might call “Limit Thinking.” This abstract approach forces one to focus solely on the features of a system essential for its performance, so that one can make predictions or evaluations, regardless of the specifics of how each individual system is built. It grounds problems in mathematics — as one cannot calculate limits without being precise about what is being measured and in what units. Once such calculations have been determined, they often drive rapid progress, signaling not only when we have reached diminishing returns, but also just how far we can aspire.

To understand the power of this approach, let’s begin with engines, returning to the work of Nicolas Léonard Sadi Carnot.

{{signup}}

Carnot, named after the Persian poet Saadi, was born in Paris in 1796 and attended the École Polytechnique before serving as an officer in the engineering arm of the French army. In 1819, at the age of 22, he took a part-time job in the army at half pay as a travailleur scientifique (scientific worker) and attended lectures at the Sorbonne, the Collège de France, and the Conservatoire des Arts et Métiers in his spare time. It was during this period that Carnot’s interest turned to heat engines.

In 1824, when Carnot was just 28 years old, he published Reflections on the Motive Power of Fire and on Machines Fitted to Develop this Power, in which he aimed to determine the fundamental limits of how heat could be converted into mechanical work. This 118-page booklet, of which he printed 600 copies at his own expense, represents essentially the whole of his scientific output (regrettably, Carnot died at 36 years old from a combination of scarlet fever and cholera). Reflections was largely ignored until 1834, when the French engineer and physicist Émile Clapeyron highlighted its importance in his own work, Memoir on the Motive Power of Heat.¹

Carnot’s work showed that what mattered for the efficiency of a heat engine was the temperature differential between the hot and cold reservoirs, rather than any particular design feature. He says of the motive power of heat: “Its quantity is fixed solely by the temperatures of the bodies between which it is effected.” In retrospect, this simple fact explained why the Watt engine was superior to the Newcomen engine; the separate condenser allowed for a larger difference between the reservoirs.

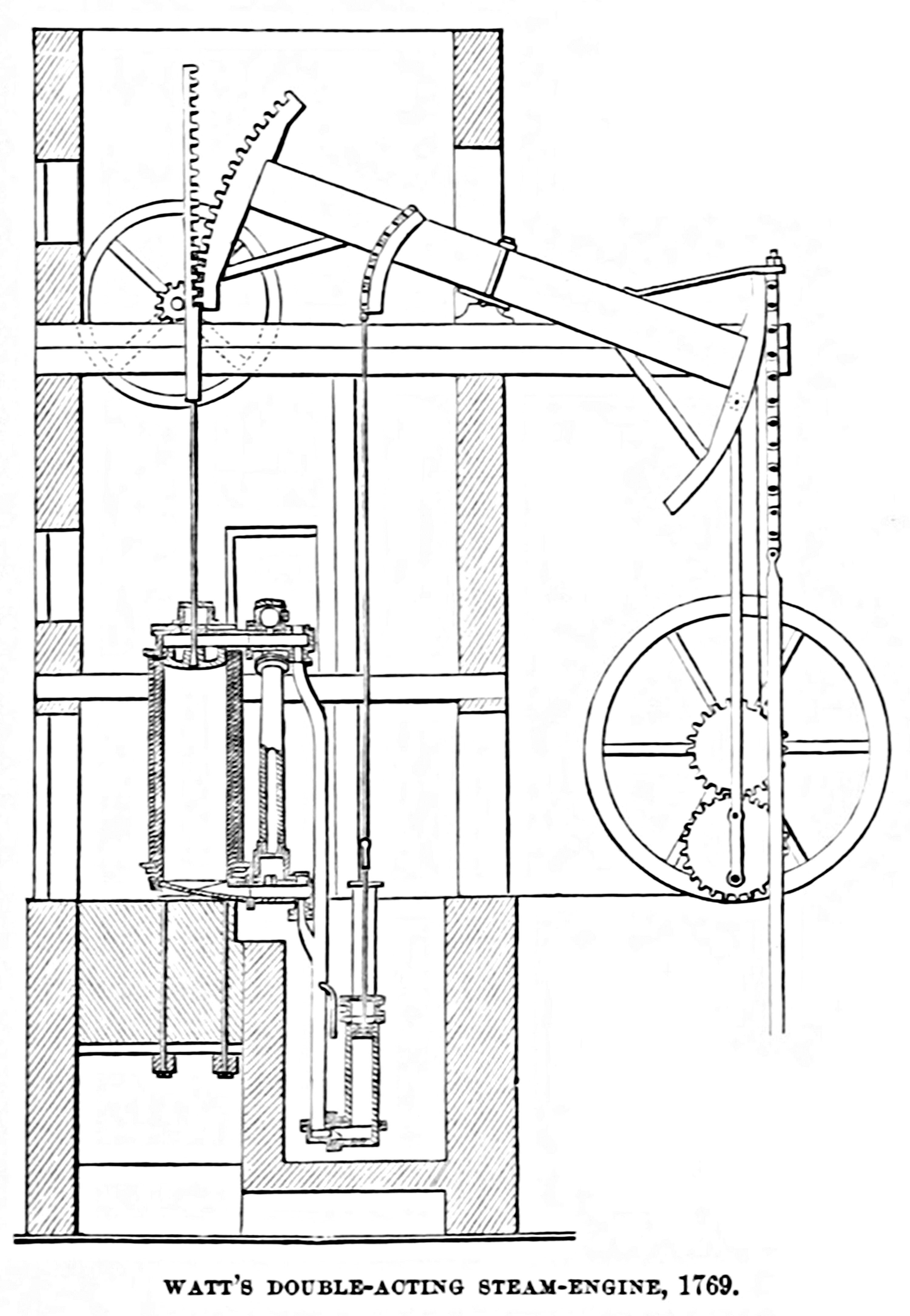
Carnot’s work would go on to inspire not only Clapeyron but also a generation of prominent physicists such as Rudolph Clausius, James Joule, and Lord Kelvin himself. It laid the groundwork for the modern theory of thermodynamics and even presented an outline of what would later become its second law. Otto Diesel directly refers to the theory of Carnot² as the rationale for his design of the engine that now bears his name (a design which achieved an efficiency of an astounding 26 percent when first tested in 1897). While the 65 years between Newcomen and Watt had seen efficiency improve roughly two percent, in the 65 years after Carnot, it leaped by about 23 percent and has climbed steadily higher even since.

125 years after Reflections, another engineer, Claude Shannon, was working at Bell Telephone Laboratories on a different practical problem: how to make telephone conversations clearer. Long-distance calls were plagued by distortion and static; amplifiers added noise, cables weakened signals, and cross-talk muddled speech. Engineers could tinker with hardware, but they lacked any way to quantify “clarity” itself — a measure of how much of a message survived its transfer from sender to receiver. Shannon reframed this into a Limit problem: not how to send more information, but how much information could ever be sent through any noisy channel.

In answering this, Shannon defined information mathematically, in terms of entropy, and calculated the maximum rate at which a noisy channel can transmit data with negligible error — the “Shannon limit.” After nearly a decade of work, his 1948 paper, “A Mathematical Theory of Communication,” established the discipline of information theory and laid the groundwork for digital communication.

The limits of thermodynamics and information theory have proven robust enough to be codified into laws and theorems that continue to influence their respective fields. But in biology, such limits have been harder to find. Living systems are messy, adaptive, and often seem to violate our expectations. Even if it is challenging to apply Limit Thinking to biology, it’s worth attempting, as it helps biologists home in on the units, models, and general principles that point us toward new ways of thinking.

Two examples help illustrate this.

For decades, enzymologists believed that the speed of a chemical reaction was limited by how fast substrate molecules could find each other by diffusion. For a one-molar solution of enzymes and substrates (an extremely concentrated amount), this diffusion limit was thought to be about 100 million to 1 billion collisions per second.

But in the early 1970s, when biochemists began directly measuring how transcription factors bind to their target sequences on DNA, some appeared to exceed this supposed speed limit. The paradox was that the diffusion limit had been derived for motion in three dimensions, yet DNA confines this search to fewer dimensions and so the limit is actually much higher. It was thus proposed that molecules could restrict the dimensionality of their search and thus achieve effective rates beyond what theory predicted. This discrepancy alerted biochemists to the need to update their models.

And, indeed, they did: By the late 1980s, free-diffusion of a transcription factor to its genomic target was replaced with a combination of one-dimensional sliding along DNA, and occasional hopping between strands. The behaviors predicted by this model were observed directly in 2007 using a fluorescently labelled lac repressor.

Another example that reveals the utility of Limit Thinking for biology is error rates.

In 1972, after a stint at Bell Labs, physicist John J. Hopfield was thinking about the limits of molecular recognition; specifically, how molecules find the correct partner amid a sea of similar ones. It was well known at the time that biology used macromolecules to assemble basic building blocks into complex polymer proteins. This relied on the “genetic code,” which translates a sequence of nucleic acids into a sequence of amino acids. Hopfield recognized that to be a useful code, the assembly process must use physics to preferentially associate the correct amino acid with its correct triplet of nucleic acid bases. His major insight was to ask: “How accurate can such a process possibly be?”

According to classical thermodynamics, the error rate should depend only on the difference in binding energy between correct and incorrect pairs. But when Hopfield did the math, biology turned out to be about a thousand times more accurate than any equilibrium model allowed. Something fundamental was missing.

The only way to beat the equilibrium limit, Hopfield realized, was to drive the system out of equilibrium — to spend energy to enforce correctness. Hopfield proposed a mechanism in which enzymes use chemical energy (from ATP hydrolysis, for example) to make certain steps irreversible, effectively giving molecules a second chance to “proofread” before committing to an error. He called this process “kinetic proofreading.”

This idea marked a turning point. It showed that biological accuracy arises not from perfect, efficient binding but, counter-intuitively, from active, energy-consuming processes that operate out of equilibrium.

Like the heat engine and the information channel, kinetic proofreading is an abstract model. And because it is agnostic to the details of exactly how it is implemented, the same underlying theory has been used to explain not only error correction in protein synthesis, but also proofreading in nucleic acid copying, antigen discrimination in the immune system, and even the dynamics of how microtubules can rapidly reorganize the cytoplasm when necessary.

Kinetic proofreading has also inspired new iterations of Limit Thinking. When it was noticed that the highest accuracy limits are only achieved when the process becomes exceedingly slow and energetically expensive, researchers began to map the limits of the trade-offs between speed, accuracy, and energy use.

Hopfield is well known for his work on proofreading, but is perhaps even better known for his work on artificial neural networks, often called Hopfield networks, for which he was awarded a Nobel prize in 2024. In his Nobel lecture, Hopfield acknowledges the role his work on proofreading played in his thinking about neural networks.

This 1974 paper was important in my approach to biological problems, for it led me to think about the function of the structure of reaction networks in biology, rather than the function of the structure of the molecules themselves. Six years later, I was generalizing this view in thinking about networks of neurons rather than the properties of a single neuron.

The Hopfield neural network, like the biomolecular networks that influenced it, also lent itself to Limit Thinking. Once formalized, it was clear to Hopfield that his associative networks could not store memories densely enough. The theory put a limit on how many memories a given number of neurons could store, but a real biological network could apparently store much more than that. Despite their utility, Hopfield’s model still lacked something essential, and this recognition, based on Limit Thinking, has led to Hopfield’s recent work on dense associative memories.

Ultimately, Limit Thinking is about how to frame problems well. Not every abstraction is useful, but if an abstraction allows you to say something quantitative about the fundamental limits of a system, you’re probably on the right track.

Carnot understood this better than anyone. “The motive power of heat,” he wrote, “is independent of the agents employed to realize it,” and “the quantity of caloric absorbed or relinquished is always the same, whatever may be the nature of the gas chosen.” Those statements freed generations of engineers to tinker with any mechanism they liked, as long as it increased the temperature differential between reservoirs.

It’s easy to forget that, in Carnot’s time, it wasn’t obvious whether such a limit even existed. Carnot notes:

The question has often been raised whether the motive power of heat is unbounded, whether the possible improvements in steam-engines have an assignable limit — a limit which the nature of things will not allow to be passed by any means whatever; or whether, on the contrary, these improvements may be carried on indefinitely.

To define a limit is not to set an arbitrary boundary but to understand the possible bounds of any given system. Carnot’s limit turned heat into a science; Shannon’s turned communication into information; Hopfield’s turned chemistry into computation. Each began with a simple question about what nature would allow and ended with a new theory that progressed technology. Apparently, searching for limits is precisely what removes them from scientific advancement as a whole.

{{divider}}

David Jordan is a researcher and founder of the Living Physics Lab, based in Cambridge, UK, and funded by the UK’s Funded by the Advanced Research + Invention Agency (ARIA) through project code NACB-SE01-P03.

Thanks to Isabelle Zane, Somsubhro Bagchi, and the ARIA Innovator Circles Programme. Thanks to Xander Balwit and Niko McCarty for editing this essay, and Ella Watkins-Dulaney for many fact-checking questions and for making the header image.

Cite: Jordan, David. “The Power of Limit Thinking.” Asimov Press (2025). DOI: https://doi.org/10.62211/63ok-78ht

Further Reading:

1. Rolt, L. T. C., and Allen, John Scott. The Steam Engine of Thomas Newcomen. United Kingdom, Moorland Publishing Company, 1977.
2. How Claude Shannon Invented the Future, Quanta Magazine

Footnotes

1. English translations of both can be found in Reflections on the Motive Power of Fire from Dover Books.
2. English translation can be found in Theory And Construction Of A Rational Heat Motor by Rudolf Diesel.