‍

Microbes are so small that tens of thousands could fit in the space of the period at the end of this sentence. And yet, for two of the most widely studied kinds — S. cerevisiae and E. coli — we know their weight with remarkable precision: A single yeast cell weighs about 100 picograms and a single E. coli bacterium weighs about one picogram, or 60 million times less than a grain of sand.

At first blush, measuring the weight of a single cell seems an impossible task. How can we make such a precise measurement with reasonable certainty? A typical kitchen scale has a sensitivity of 0.1 grams, meaning it can detect the difference between a banana weighing 175 grams and another weighing 175.1 grams. By contrast, an E. coli cell weighs 100 billion times less than 0.1 grams.

Today, such measurements are made using profoundly clever contraptions developed by scientists over the last couple of decades. These devices can measure individual cells with femtogram precision (a unit 1,000-times smaller than a picogram). But before such precision instruments, scientists had to make do with whatever was already in the lab.

{{signup}}

Back in 1953, for example, two biologists from Southern Illinois University (supported, in part, with funding from the Anheuser-Busch brewery)¹ invented one of the first methods to determine the weight of an individual yeast cell. And they did it, incredibly, using little more than a microscope, sugar water, and a camera.

Their method made use of Stokes’ law, which describes how a small sphere sinks through a liquid. If the sphere falls without causing turbulence, the liquid “pushes back” with a drag force. In 1845, Sir George Stokes — an Irish mathematician and the longest-serving Lucasian Professor of Mathematics at the University of Cambridge — showed that this drag force is proportional to the sphere’s size, the liquid’s viscosity, and the sphere’s velocity through the fluid. Written as a formula, where r is the sphere’s radius, η is the fluid’s viscosity, and v is the velocity at which the sphere sinks:

Now, this is just the equation for drag force, or the amount of resistance that the fluid exerts on the sphere. But the sphere is also acted on by gravity, which pulls it down, and by buoyancy, which pushes it up! The downward pull is given by the sphere’s weight minus the buoyant force:

Here, d₁​ is the sphere’s density, d₀ is​ the fluid’s density, and g is gravity. At terminal velocity — meaning, when the sphere falls through the liquid at a steady speed — the downward net force is exactly balanced by the upward drag force. So we can set the two equations against one another to arrive at a final equation:

The brilliance of this equation is that it enables us to figure out the mass of the sphere. All we need to measure is the sphere’s radius, its velocity through the fluid, and the viscosity and density of that fluid. Once those values are known, we plug them into the equation to calculate the sphere’s density. Finally, we multiply this density by the sphere’s volume (determined from its radius) to arrive at a mass.

And that’s exactly what the Southern Illinois researchers did, back in 1953, to figure out the mass of individual yeast cells.

The researchers suspended the cells in a one percent sugar water solution, placed the samples onto a microscope slide, and then propped the slide up vertically. Next, they used a microscope and camera to film time-lapse videos of the yeast cells falling, frame by frame. They did this for 67 of these cells at 400x magnification.

From the photos, the researchers could measure the distance each cell traveled over a fixed time, determining the radius of each using a scale bar. And then — because they already knew the fluid’s viscosity and density — they were able to use Stokes’ law to calculate the weight of an individual cell: 79 picograms, on average: a value remarkably close to estimates made as recently as 2022.

The researchers proceeded as if each yeast cell were spherical — an important assumption because Stokes’ law works only for spheres moving through a fluid. The symmetry of a sphere is what enables an exact calculation of the drag force. And yeast cells, being nearly spherical in real life, mapped onto the assumption well enough for the math to hold.

But not all cells are spheres. E. coli cells, for example, look more like elongated rods. If you were to perform the 1953 experiment on them, the cells would create turbulence, throwing off Stokes’ equations. Measuring a cell like this, therefore, requires a completely different strategy.

‍

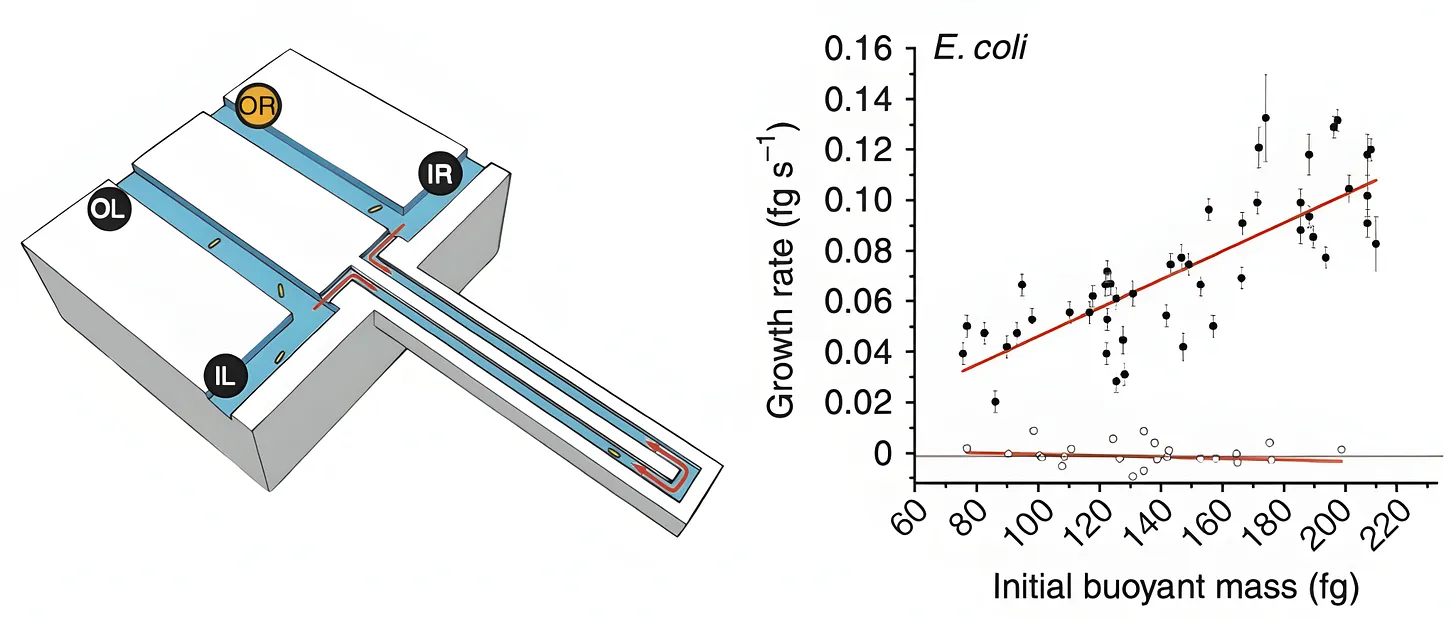
In 2010, MIT scientists came up with a tool for measuring the mass of any single bacterial cell, including E. coli. The device, called “a suspended microchannel resonator,” is basically a “hollow microcantilever beam containing an embedded fluidic microchannel.” The beam has a U-shaped tunnel running through its interior and vibrates very quickly, similar to a guitar string.

As a single cell floats through the channel in this beam, the beam’s vibration changes ever so slightly. Heavier cells shift the frequency more. Those frequency shifts are what allow researchers to figure out the cell’s “buoyant mass,” or how much heavier the cell is compared to water.² Such measurements have femtogram precision, meaning they can detect changes between two masses 1,000-times smaller than a bacterium’s weight.

The device can also be used to measure the same cell again and again, meaning researchers can track the growth of the cell over time. After a cell passes through the vibrating beam and its mass is recorded, researchers reverse the flow of liquid and send it back through the channel in the opposite direction. If the procedure is repeated quickly and often enough, the cell becomes trapped at the end of the vibrating beam. Each pass yields a new frequency measurement and, as the cell grows, the frequency shift increases proportionally to its added mass.

When the authors measured 48 individual cells and averaged the results, they found that a typical E. coli weighs about 0.55 picograms. But this number is constantly in flux because the growth rate increases in proportion to cell size. At 37 °C, the smallest cells added about 0.06 picograms of mass per hour, while the largest gained closer to 0.14 picograms per hour.

The beauty of these experiments is how they bring basic mathematics to bear on biology. The yeast experiment, in particular, evokes the famous 19th-century work by Lord Rayleigh, in which he calculated the size of a single molecule using only oil and water.

In 1890, Rayleigh realized that the thickness of a molecular film could be found by dividing its volume by the area it covered. In his at-home laboratory, Rayleigh placed a small droplet of oil onto a calm water surface and watched the oil spread into an impossibly thin sheet. By measuring the surface area that the drop covered, he calculated the film’s thickness as 1.6 × 10⁻⁷ centimeters, and correctly deduced this to be the length of a single oil molecule. Impressively, Rayleigh’s estimate was off by just 18.5 percent when benchmarked against modern measurements of those same molecules, made using X-rays and sophisticated equipment.

All of these experiments share the same quality: They take a phenomenon that seems difficult to measure and overcome this difficulty through mathematics and first principles thinking. Such experiments are timeless; a reminder that we don’t have to overcomplicate either our tools or our questions to make immense contributions to biology. Cells are physical objects — collections of molecules with real weights, shapes, and speeds. Think of them as such, and anything can be measured.

{{divider}}

Niko McCarty is a founding editor of Asimov Press.

Cite: McCarty, N. “The Weight of a Cell.” Asimov Press (2025). https://doi.org/10.62211/51hg-87ty

Footnotes

1. Breweries have been patrons of yeast science for more than a century. In 1876, the Carlsberg Laboratory in Copenhagen became one of the first industrial labs devoted entirely to brewing research, leading to the isolation of Saccharomyces pastorianus, the species used to make lager beer.
2. The beam is first calibrated using polystyrene beads of a known size and density. A laser sensor measures the beam’s vibrations, which, based on the calibration measurements, help determine the mass of individual cells.